Rendering was done in OpenDX.
This demo solves the Helmholtz equation in a dinosaur shaped domain. The unstructured mesh has 826 triangles.

Here the Helmholtz equation (with k = 2*pi) is solved on a realistic plasma and limiter geometry. Dirichlet boundary condition are set to 1.0 on the plasmaand 0.0 on the limiter. The unstructured mesh has 556 triangles.

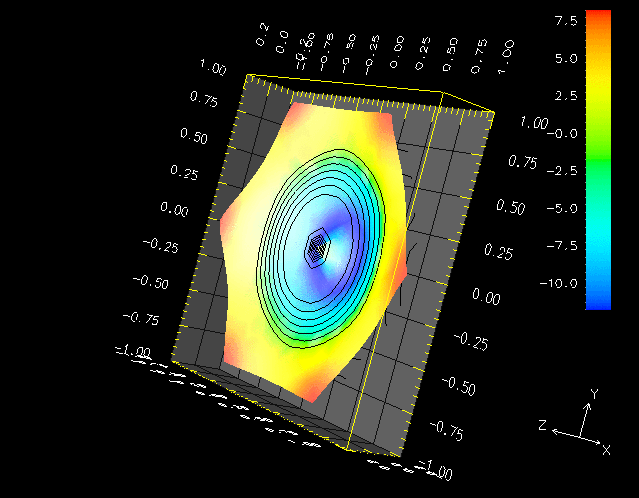
Complex eigenvalue problem. The equation is of Helmholtz type with zero Dirichlet conditions on the internal boundary and phase shifted conditions on the outer edges. Represented is a higher order mode: the surface height corresponds to the mode amplitude whereas the colored contours represent the phase. Regions with accumulation of red-blue contours are associated with a phase transition from pi to -pi. Rendering in OpenDX.

Solve Helmholtz's equation on a hexagonal shaped domain to recover Christopherson's well known pattern cell solutions. (D G Christopherson, Quart. J. of Math., 11, 63-65 (1941)). The unstructured mesh has 675 triangles.